δ oder Δ
Delta behandelt die Beziehung zwischen der Veränderung im Optionspreis und der Veränderung im Preis des Basiswertes
\( δ=\frac{\Delta c}{\Delta S} \)
oder \( Delta = \frac{Optionspreis\ddot{a}nderung}{Basiswertpreis\ddot{a}nderung} \)
Im Black Scholes Modell entspricht das Delta annäherungsweise dem \( N(d_{1}) \) für den Call sowie \( N(d_{1}) \) – 1 für den Put. Wie wir bereits wissen, können wir N(d) aus der Tabelle der Normalverteilungen ablesen.
Zudem hilft das Black Scholes Modell dabei, mithilfe von Delta ein risikoneutrales Portfolio aufzubauen. In der Fachterminologie wird das auch als “dynamisches Hedging” bezeichnet. Dabei werden der Basiswert sowie eine bestimmte Anzahl Optionen so kombiniert, dass sich die Deltas der beiden Seiten gleichen. Das Delta einer Aktie ist immer +1, ist man die Aktie short so hat man ein Delta von -1. Das Delta eines Calls liegt zwischen 0 und +1, das Delta eines Puts liegt zwischen -1 und 0.
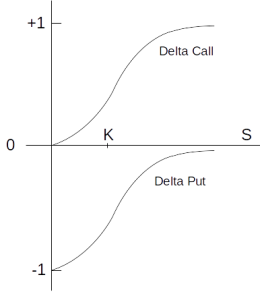
Das Delta ist die Steigung der Optionspreiskurve.