Das Binomialmodell ist eine sehr intuitive und anschauliche Art, Optionen zu bewerten, und wird deshalb auch gerne im Unterricht eingesetzt. Es veranschaulicht die mögliche Preisentwicklung von Periode zu Periode.
Am besten sieht man das anhand eines Beispiels. Wir kaufen uns eine Call Option auf eine Aktie mit folgenden Parametern:
• Kauf 1 Call auf Aktie X
• Laufzeit 1 Monat
• Strike 10 Euro
• Aktienkurs aktuell 9 Euro
Nach einem Monat kann der Aktienkurs entweder auf 11 Euro gestiegen oder auf 7 Euro gefallen sein. Ist er auf 11 Euro gestiegen, hat unsere Option einen Wert von 1 Euro. Ist der Kurs hingegen gefallen, ist unsere Call Option wertlos geworden. Grafisch im Binomialbaum sieht das folgendermaßen aus:
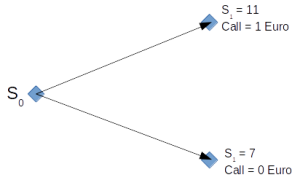
Wichtig ist nun, dass man ein sogenanntes risikoloses Portfolio erreichen muss, also eines, in dem ein Investor ein bestimmte Menge an Aktien sowie eine bestimmte Menge an Optionen hält, und gleichgültig, ob der Aktienkurs nach Ende unserer Betrachtungsperiode gestiegen oder gefallen ist, für den Investor insgesamt das gleiche Ergebnis entsteht. Der Investor soll also in unserem Beispiel nach einem Monat finanziell immer exakt gleich da stehen, gleichgültig, ob der Preis unserer Aktie nun auf 11 Euro gestiegen oder auf 7 Euro gefallen ist. Als Beispiel nehmen wir ein Portfolio aus Aktien und einem short Call.
Dafür setzen wir zunächst die beiden Ergebnisse zueinander gleich. Wir gehen davon aus, dass beide Ergebnisse gleich wahrscheinlich sind.
\( 11S_{1}-1=7S_{1} \) \( S_{1}=0,25 \)Wir benötigen für unser risikoloses Portfolio 0,25 Aktien und verkaufen dagegen 1 Call Option. Dadurch ist der Endwert für den Investor immer gleich, ob der Preis der Aktie nun auf 11 steigt oder auf 7 fällt. Der Investor hat immer ein Ergebnis von 1,75 Euro.
Um die Sache auch aus heutiger Sicht betrachten zu können, müssen wir noch den Barwert unseres risikolosen Portfolios bilden. Das Ergebnis wird dafür mit dem risikolosen Zinssatz abgezinst. Angenommen, der risikolose Zinssatz beträgt 1% und wir zinsen für die Dauer von einen Monat ab, ergibt sich folgendes Ergebnis:
\( 1,75 * e^{-0,01*1/12}=1,7485 \)Nun können wir relativ einfach den Preis der Option daraus ableiten. Wir kennen bereits den heutigen Aktienkurs. Dieser ist 9 Euro. Wir haben 0,25 Aktien. Diese sind somit 9 * 0,25 = 2,25 Euro wert. Unser Portfolio ist aus Aktien und Optionen ist aus heutiger Sicht 1,7485 Euro wert. Der Unterschied zwischen diesen beiden Werten ist unser Optionspreis:
Optionspreis = 2,25 – 1,7485 = 0,5015 Euro
Der Optionspreis muss also bei 0,5015 Euro liegen, ansonsten wäre eine risikolose Arbitrage möglich. Denn läge der Preis höher, könnte jemand die Option verkaufen, die Prämie zum risikolosen Zinssatz anlegen und daraus Gewinn machen. Läge der Preis tiefer, könnte jemand die Option kaufen und die Prämie günstiger über den risikolosen Zinssatz finanzieren.
Setzt man statt konkreter Zahlen universell gültige Variablen in den Baum sowie die Formel ein, ergibt sich folgendes Bild:
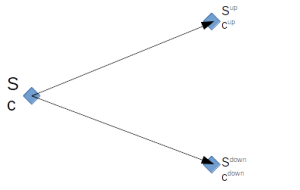
S ist dabei der Aktienpreis und c der Preis der Call Option.
Wieder betrachten wir ein Portfolio, das sich aus einer verkauften Call Option und einer noch unbekannten Menge an Aktien zusammensetzt, so, dass keine Arbitragemöglichkeit besteht. Unsere Aktie kann sich wieder entsprechend im Wert steigern, diesmal auf den generellen Wert von \( S^{up} \)
oder im Wert sinken auf den generellen Wert \( S^{down} \)
. Steigt der Preis der Aktie, ist unser Portfolio \( n*S^{up}-c^{up} \)
wert. Sinkt der Preis der Aktie, ist unser Portfolio \( n*S^{down}-c^{down} \) wert. Die Werte beider risikolosen Portfolien müssen sich wieder gleichen. Daraus ergibt sich:
Daraus können wir nun n, also die Anzahl der benötigten Aktien, berechnen:
\( n = \frac{c^{up}-c^{down}}{S^{up}-S^{down}} \)Um den Wert des Portfolios aus heutiger Sicht zu erhalten, zinsen wir wieder mit dem risikolosen Zinssatz ab. Diesen bezeichnen wir mit r. Die Zeit, um die wir abzinsen, bezeichnen wir mit T. Daraus ergibt sich nun folgender Barwert des Portfolios:
Barwert des risikolosen Portfolios = \( (n*S^{up}-c^{up})e^{-rT} \)
Das muss aber auch gleich viel sein wie die Kosten, um das Portfolio heute aus S und c aufbauen zu können. Also muss folgende Gleichung gelten:
\( n*S – c = (n*S^{up}-c^{up})e^{-rT} \)Genau daraus können wir nun den Preis unseres Calls darstellen:
\( c = n*S – (n*S^{up}-c^{up})e^{-rT} \)Wir setzen nun statt n unsere vorab erhaltene Formel \( n = \frac{c^{up}-c^{down}}{S^{up}-S^{down}} \)
ein. Daraus erhalten wir schlussendlich folgende Formel:
\( c =\left[p*c^{up}+(1-p)c^{down}\right]* e^{-rT} \)
wobei \( p = \frac{e^{rT}-down}{up-down} \)
dabei kann man p auch als die Wahrscheinlichkeit einer Aufwärtsbewegung (“up”) sehen und (1-p) als die Wahrscheinlichkeit einer Abwärtsbewegung (“down”).
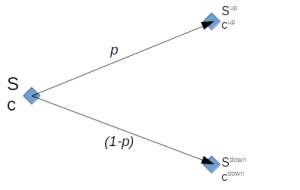
Damit kann man, wenn man die Wahrscheinlichkeiten für eine Auf- und eine Abwärtsbewegung mit einbeziehen kann und möchte, die allgemeine Formel für den erwarteten Aktienkurs mithilfe dieser definieren:
\( E(S_{T})= pS^{up}+(1-p)S^{down} \) \( E(S_{T})= pS(up – down) + S^{down} \) \( E(S_{T})= S*e^{rT} \)was soviel bedeutet wie der erwartete zukünftige Aktienkurs entspricht dem um den risikolosen Zinssatz aufgezinsten, heutigen Aktienkurs. Wichtig ist, dass sich diese Gleichung nur in einer idealen, risikoneutralen Welt bewahrheitet. In unserer realen Welt müssen in den Optionspreismodellen stets Anpassungen vorgenommen werden.